

Arithmetic Sequence (Arithmetic Progression)
GEOMETRIC SIGMA NOTATION CALCULATOR SERIES
See our sigma notation calculator for summing up series defined by a custom expression. The calculator output is a part of the sequence around your number of interest and the sum of all numbers between the starting number and the nth term of the sequence. The fibonacci sequence is fixed as starting with 1 and the difference is prespecified. Finally, input which term you want to obtain using our sequence calculator. Specify the common difference, which is how the sequence is constructed basically. Then specify the direction of the sequence: increasing or decreasing, and the number you want to start from. Start by selecting the type of sequence: you can choose from the arithmetic sequence (addition), geometric sequence (multiplication), and the special Fibonacci sequence. This is a very versatile calculator that will output sequences and allow you to calculate the sum of a number sequence between a starting item and an n-th term, as well as tell you the value of the n-th term of interest. Our sequence calculator outputs subsequences of the specified sequence around the selected nth element. If each element is larger than or smaller than the preceding element, then a sequence is strictly monotonically increasing or strictly monotonically decreasing, respectively. Sequences can be monotonically increasing - that is if each term is greater than or equal to its preceding term, or they can be monotonically decreasing, if the reverse is true. Number sequences can be expressed as the function that generates the next term in a sequence from the previous one. The number of elements is the length of the sequence. In mathematics, a sequence is an ordered list of objects, usually numbers, in which repetition is allowed. Calculating the sum of an arithmetic or geometric sequence.
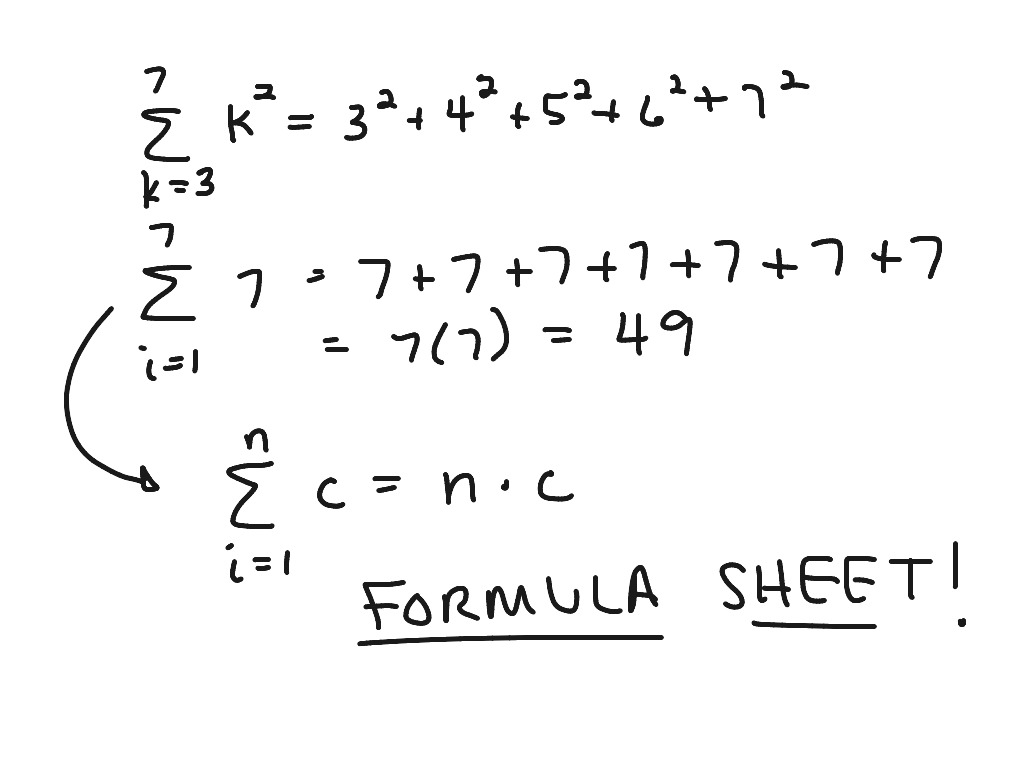
GEOMETRIC SIGMA NOTATION CALCULATOR HOW TO
How to calculate n-th term of a sequence?.Geometric Sequence (Geometric Progression).Arithmetic Sequence (Arithmetic Progression).determine (in simple cases) whether an infinite series has a sum.write down the sequence of partial sums of an infinite series.recognise the difference between a sequence and a series.In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature.Īfter reading Mathlibra’s pages of Sequences and Series, you should be able to: We also consider two specific examples of infinite series that sum to e and π respectively. We explain how the partial sums of an infinite series form a new sequence, and that the limit of this new sequence (if it exists) defines the sum of the series. In this unit we see how finite and infinite series are obtained from finite and infinite sequences. This is an infinite geometric series with first term a=1 and common ratioĮvaluating pi (π) and Euler’s number ( e) with series This is an infinite geometric series with first term a=1 and common ratio r=⅖ If possible, find the sum of each infinite geometric series. This is an infinite geometric series with a 1=⅓ and r=⅓.Īs n approaches infinity, ⅓ n approaches 0. When dividing by a fraction, you can multiply by the inverse. To find r, find the common ratio using a 1 and a 2, a 2 and a 3. 11, the series is diverges and the sum does not exists. When r, the common ratio, is strictly between -1 and 1, i.e. There is a simple test for knowing instantly which geometric series converges and which diverges. If a series does not converge, then we say that it diverges. When we sum the terms of a series, and the answer we get after each summation gets closer and closer to some number, we say that the series converges. We denote the sum of an infinite number of terms of a sequence by You might think that if you keep adding more and more terms you will eventually get larger and larger numbers, but in fact you won’t even get past 1 – try it and see for yourself! If you don’t believe this, try doing the following sum, a geometric series, on your calculator or computer: You might think that this is a silly question – surely the answer will be ∞ when one sums infinitely many numbers, no matter how small they are? The surprising answer is that while in some cases one will reach ∞ (like when you try to add all the positive integers together), there are some cases one will get a finite answer. In this section, we consider what happens when we add infinitely many terms together. Thus far we have been working only with finite sums, meaning that whenever we determined the sum of a series, we only considered the sum of the first n terms.


 0 kommentar(er)
0 kommentar(er)
